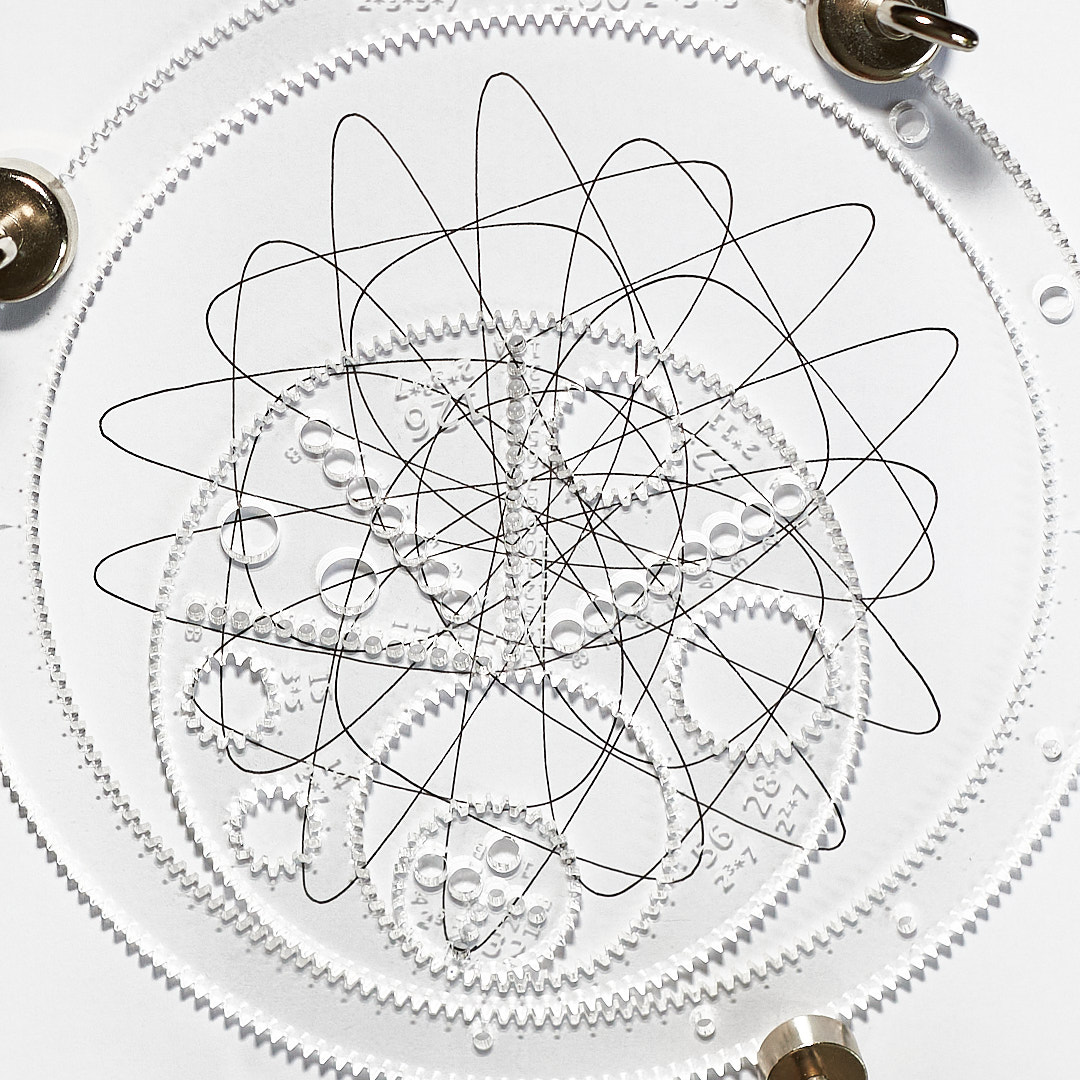
Symmetries produced by a simple system
When there are an even number of points, the axes of symmetry pass through 0 points or 2 points each. When odd, each axis passes through just one point.
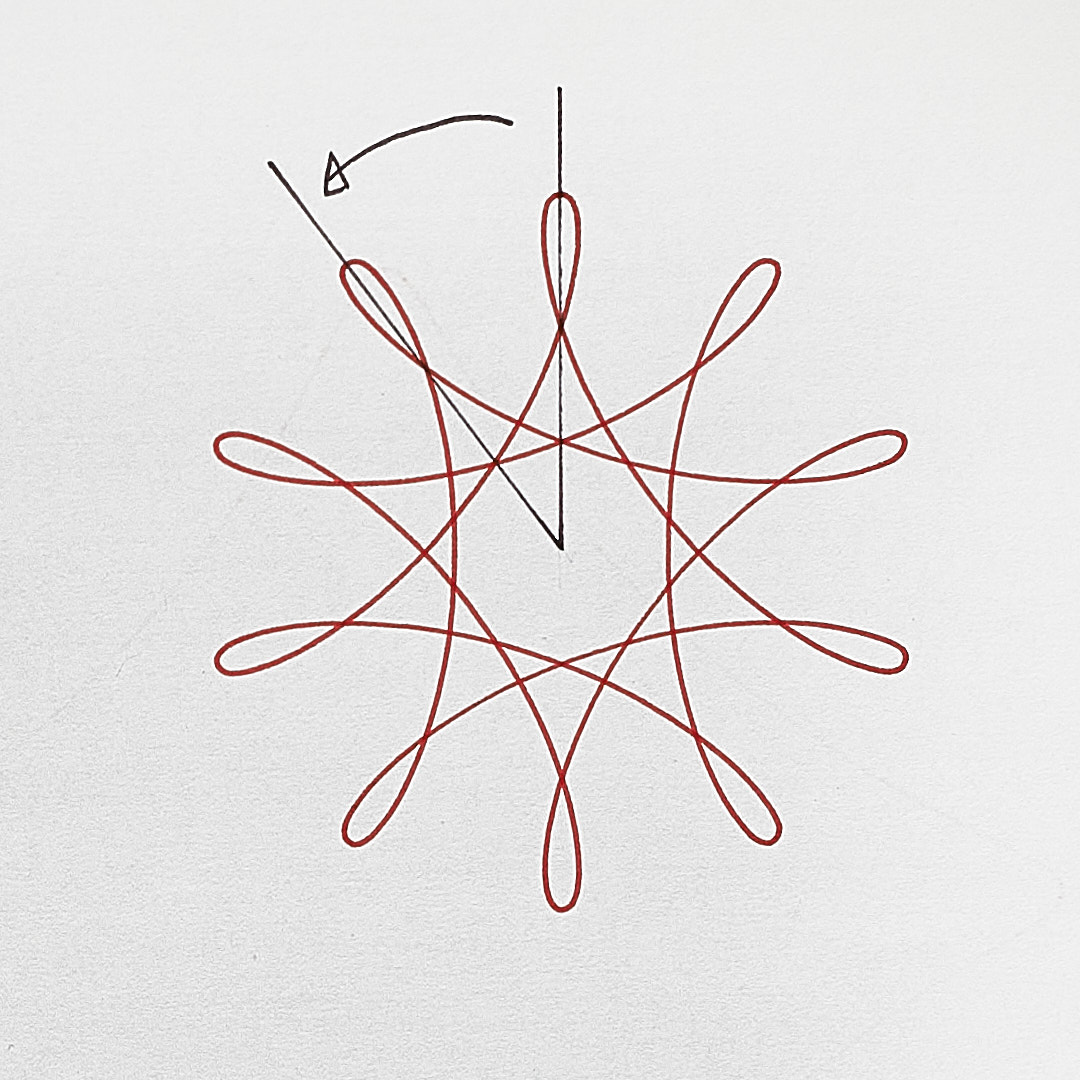
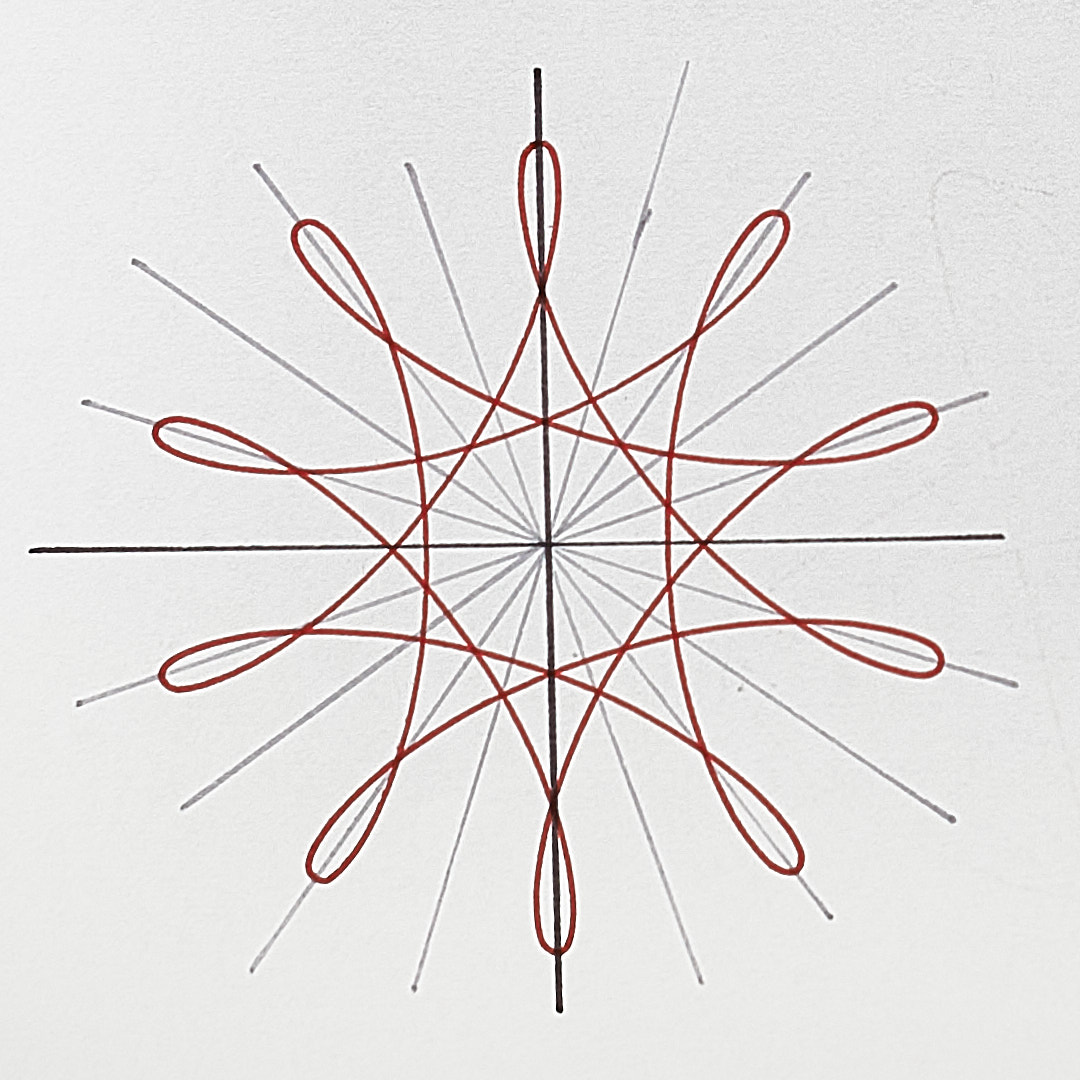

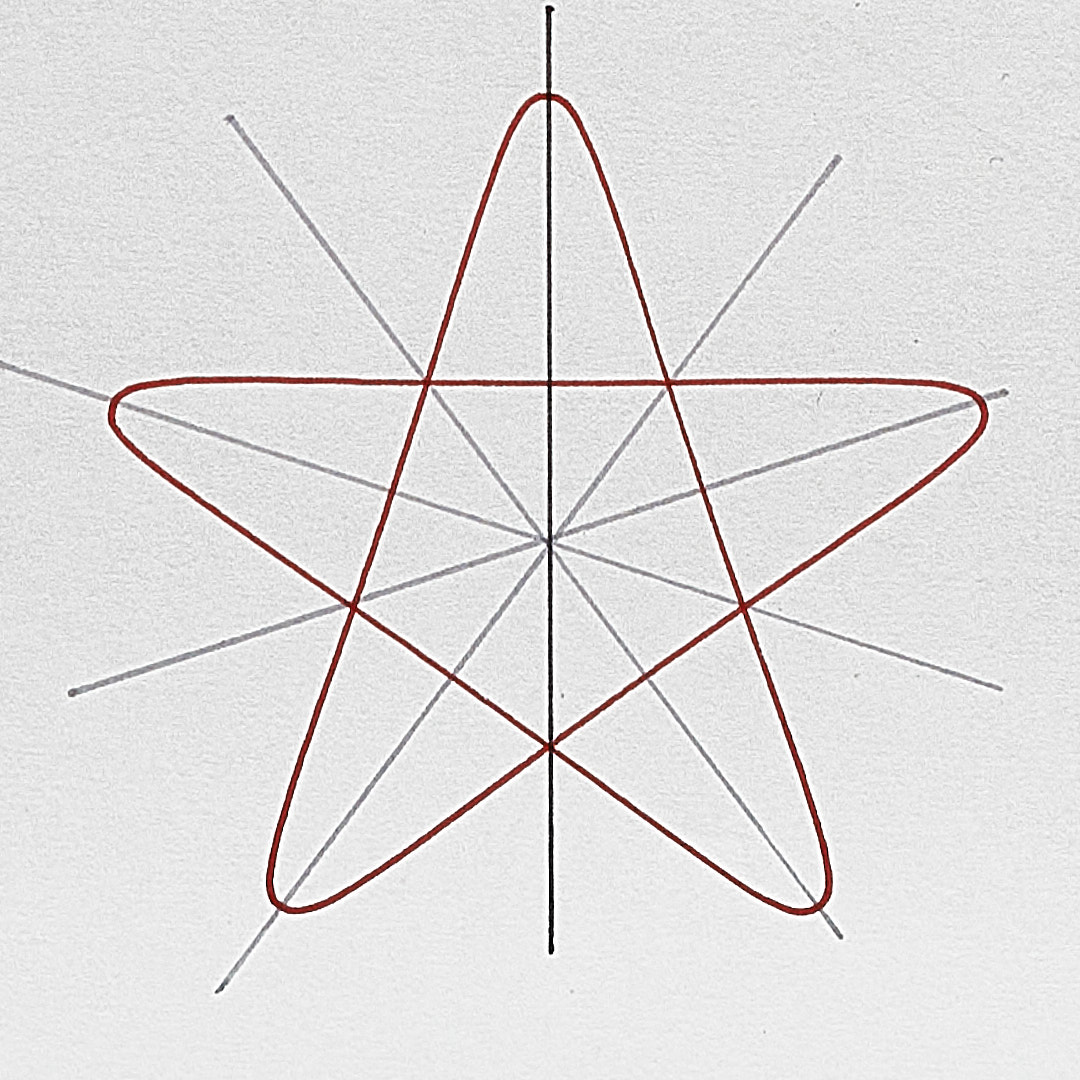
When there are an even number of points, the axes of symmetry pass through 0 points or 2 points each. When odd, each axis passes through just one point.
 Here there are 2 offset-classes, $[0]$ and $[7]$. You can see that offset-classes are a feature of 'points' of the outer system $\mathbf{AB}$ rather than a classification of rotations of $\mathbf{D}$.
Here there are 2 offset-classes, $[0]$ and $[7]$. You can see that offset-classes are a feature of 'points' of the outer system $\mathbf{AB}$ rather than a classification of rotations of $\mathbf{D}$.
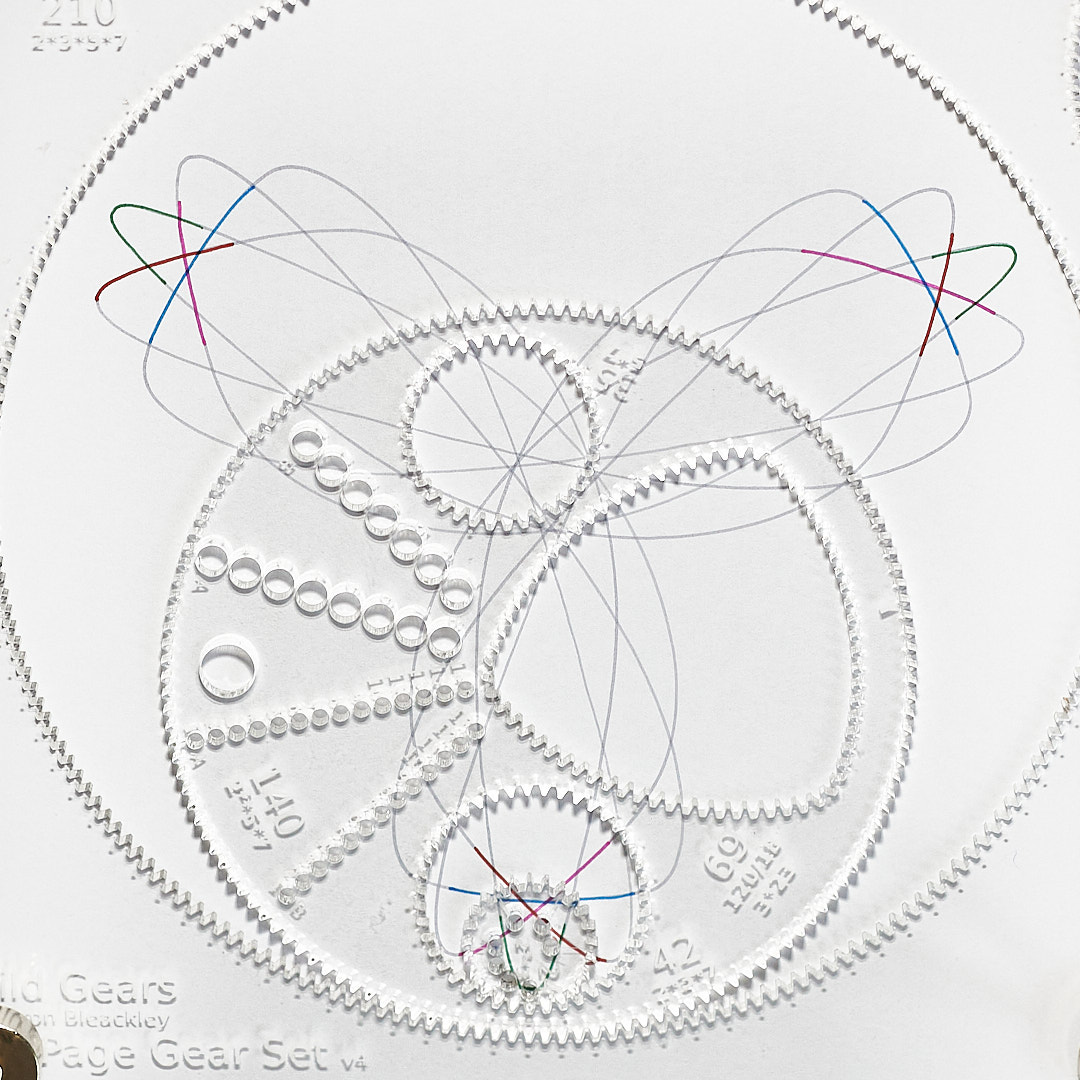 Here there are 4 offset classes. Two of them are symmetrical to each other, but correspond to $[-6] (= [18])$ and $[+6]$.
Here there are 4 offset classes. Two of them are symmetrical to each other, but correspond to $[-6] (= [18])$ and $[+6]$.

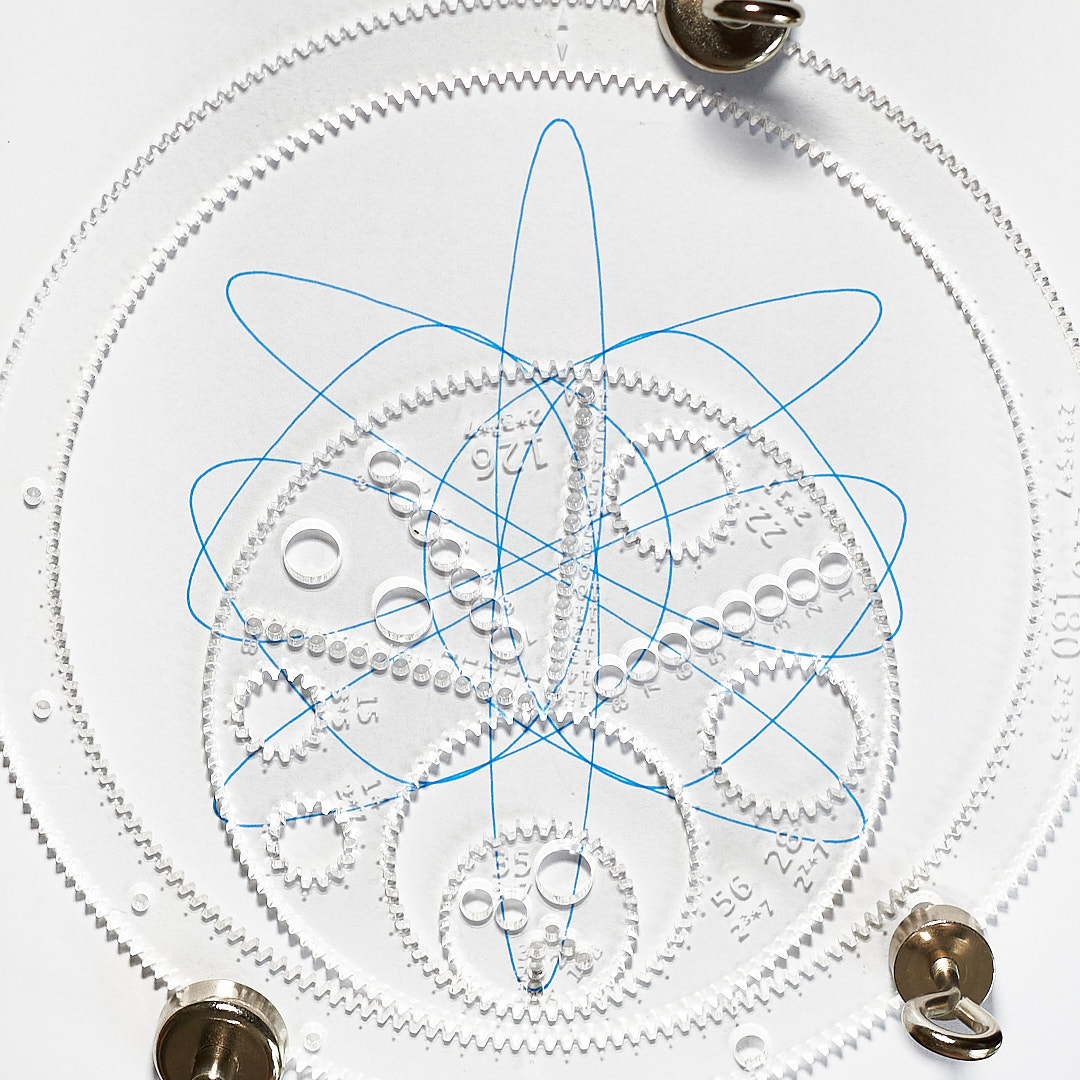


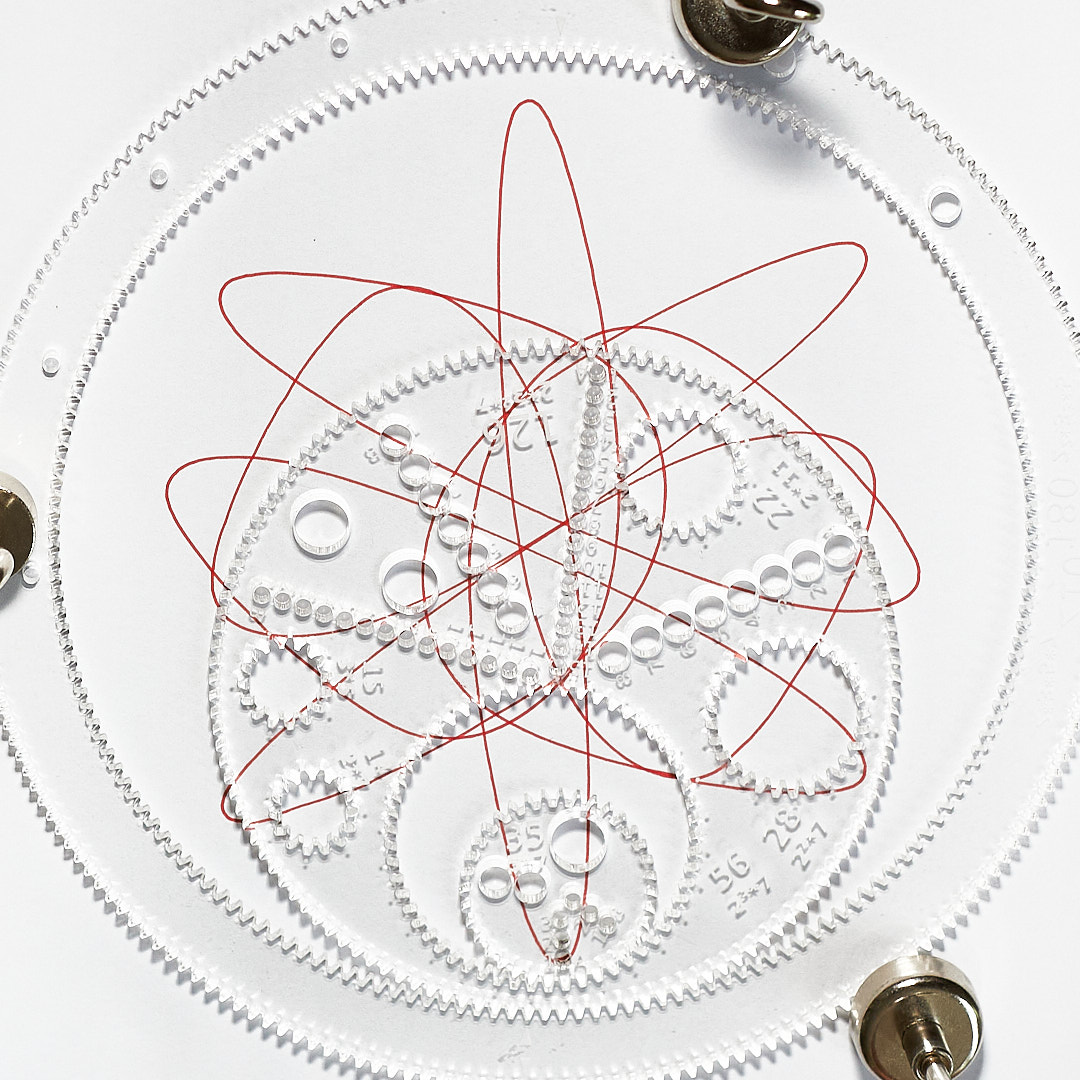
Offsetting the inner cog by $gcd(56,35)=7$ teeth induces a rotation by $r(180,126)=18$ teeth on the outer ring.
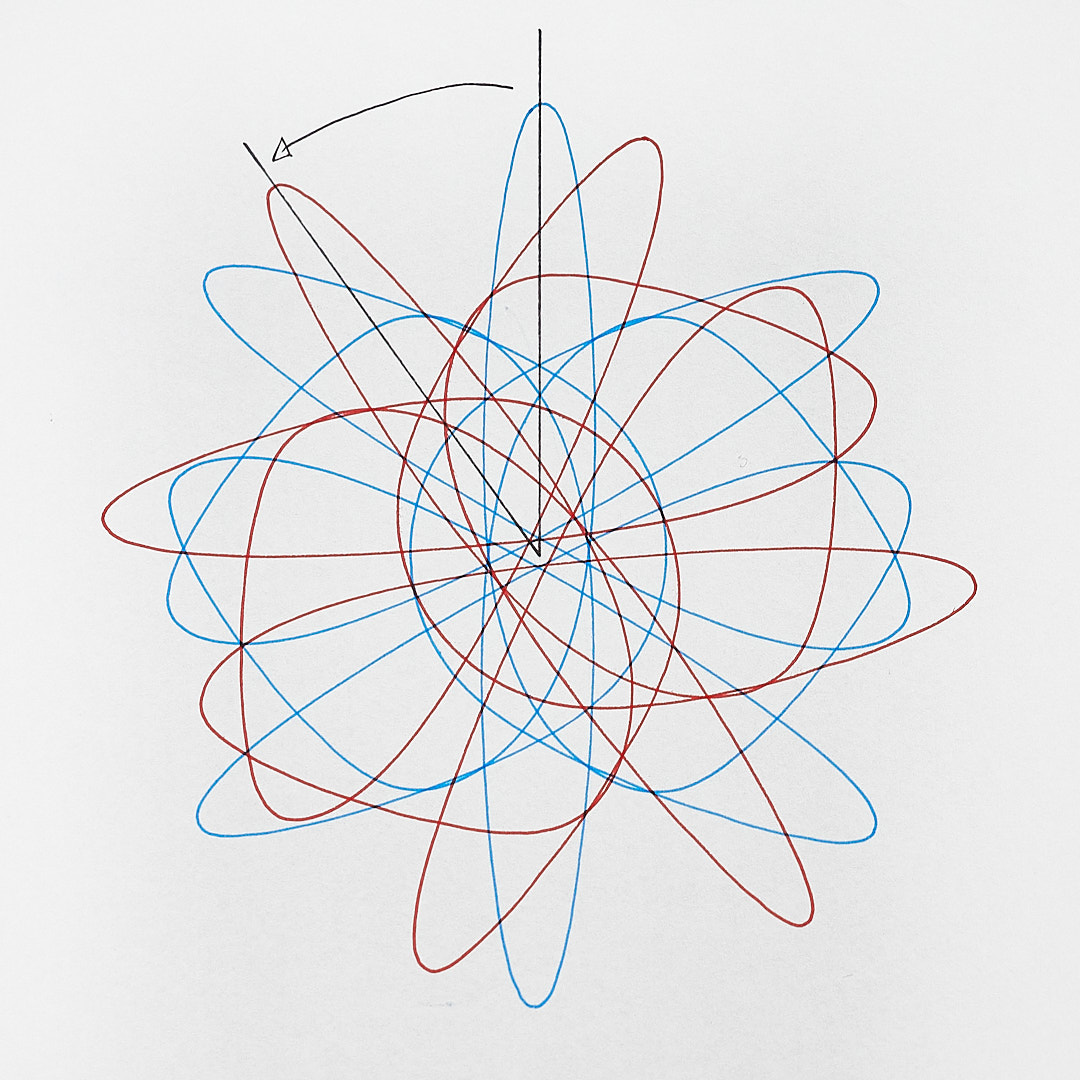
 Starting with an offset produces a curve with rotational but not reflectional symmetry.
Starting with an offset produces a curve with rotational but not reflectional symmetry.
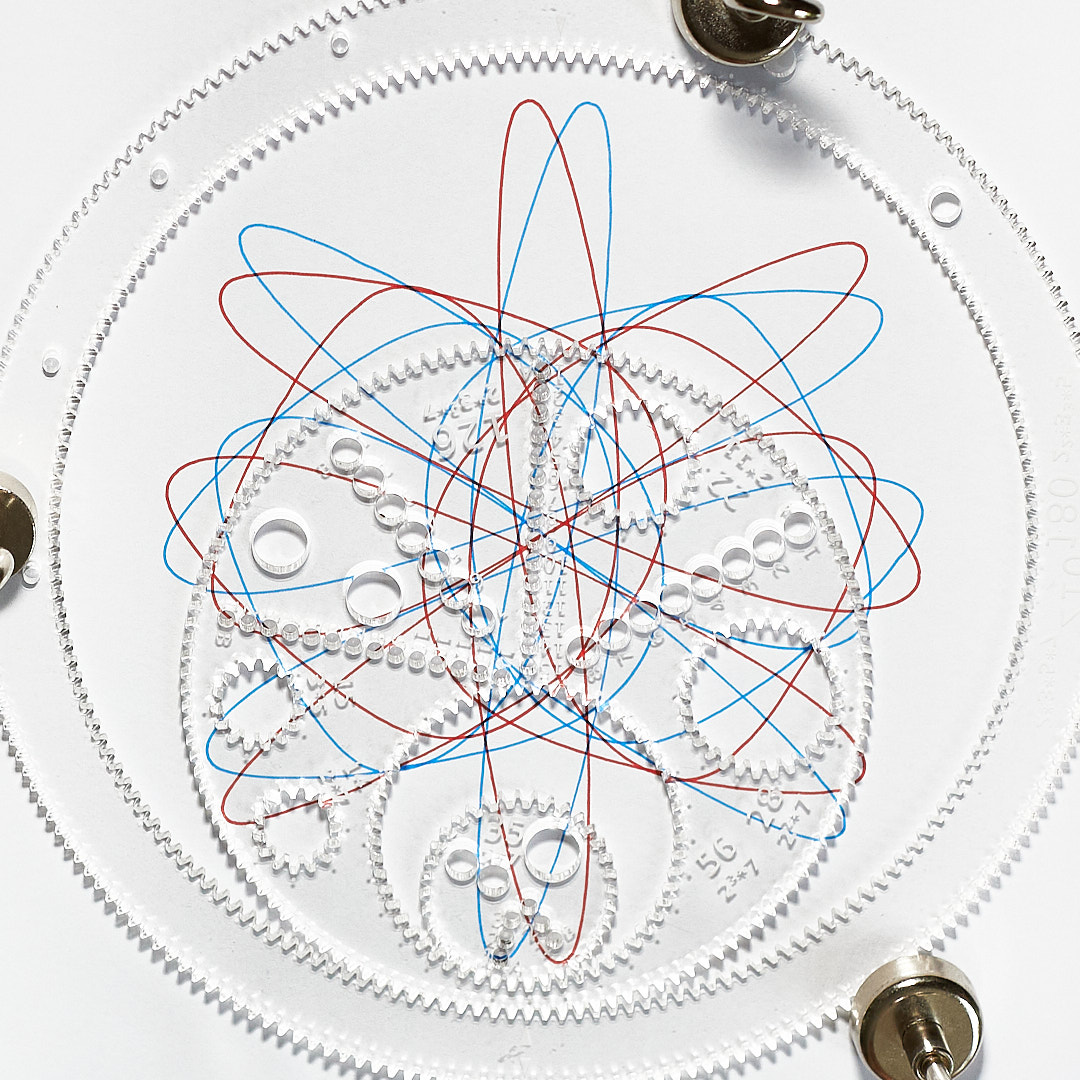 Reflecting the offset reflects the curve...
Reflecting the offset reflects the curve...
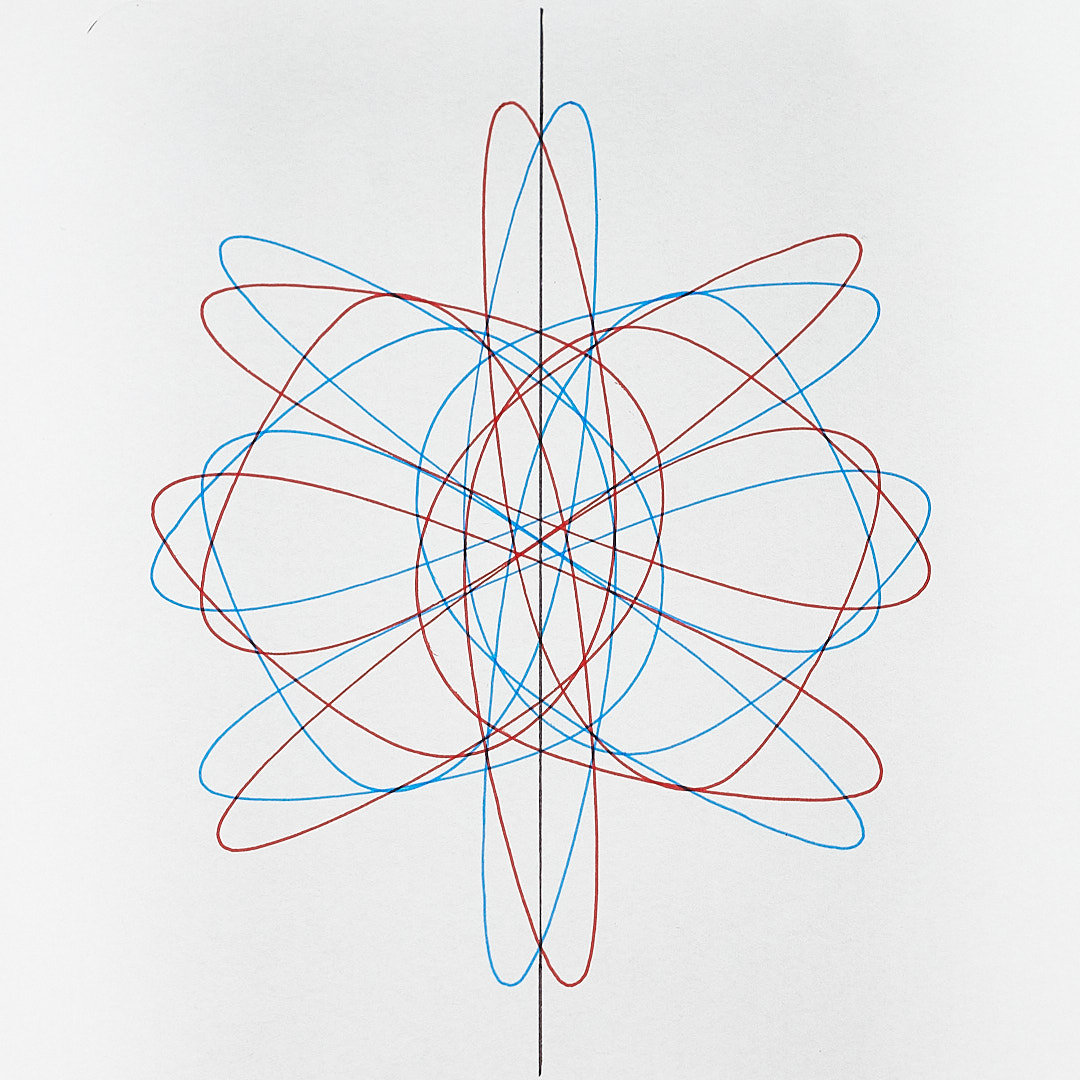 ... resulting in a figure that has reflectional and rotational symmetry.
... resulting in a figure that has reflectional and rotational symmetry.