$\DeclareMathOperator{\lcm}{lcm}$In this post, I'll derive expressions about rotations in spirograph systems.
This builds on [Aaron's Post](https://www.wildgears.com/math-and-predictions.html), which is more accessible.
A useful reference for identities for $\gcd$ and $\lcm$ is https://www.cut-the-knot.org/arithmetic/GcdLcmProperties.shtml - I suggest at least glancing over it before proceeding.
## 1 Simple Systems
Suppose a part $\mathbf{B}$ with $B$ teeth rotates against a part $\mathbf{A}$ with $A$ teeth, for example a wheel inside a ring. Each time $\mathbf{B}$ rotates one full turn relative to $\mathbf{A}$, it moves around $B$ teeth inside $\mathbf{A}$. The pattern it leaves will repeat once it returns to its starting point, i.e. when a whole number of rotations of $\mathbf{B}$ corresponds with a whole number of traversals of $A$. For example, if an 63 wheel rotates inside a 108 ring, then after 12 rotations it travels 756 teeth, which is 7 whole traversals.
Let $n, m \in \mathbb{N}$ such that $nB = mA$.
Then $m\frac{A}{B} \in \mathbb{N}$, so $B|mA$.
But $A|mA$, so $\lcm(A,B)|mA$.
Thus the minimum $n, m$ satisfying $nB=mA$ are
$$m = \frac{\lcm(A,B)}{A}$$
$$n = \frac{\lcm(A,B)}{B} = \frac{A}{\gcd(A,B)}$$
A curve produced by a simple system.
-
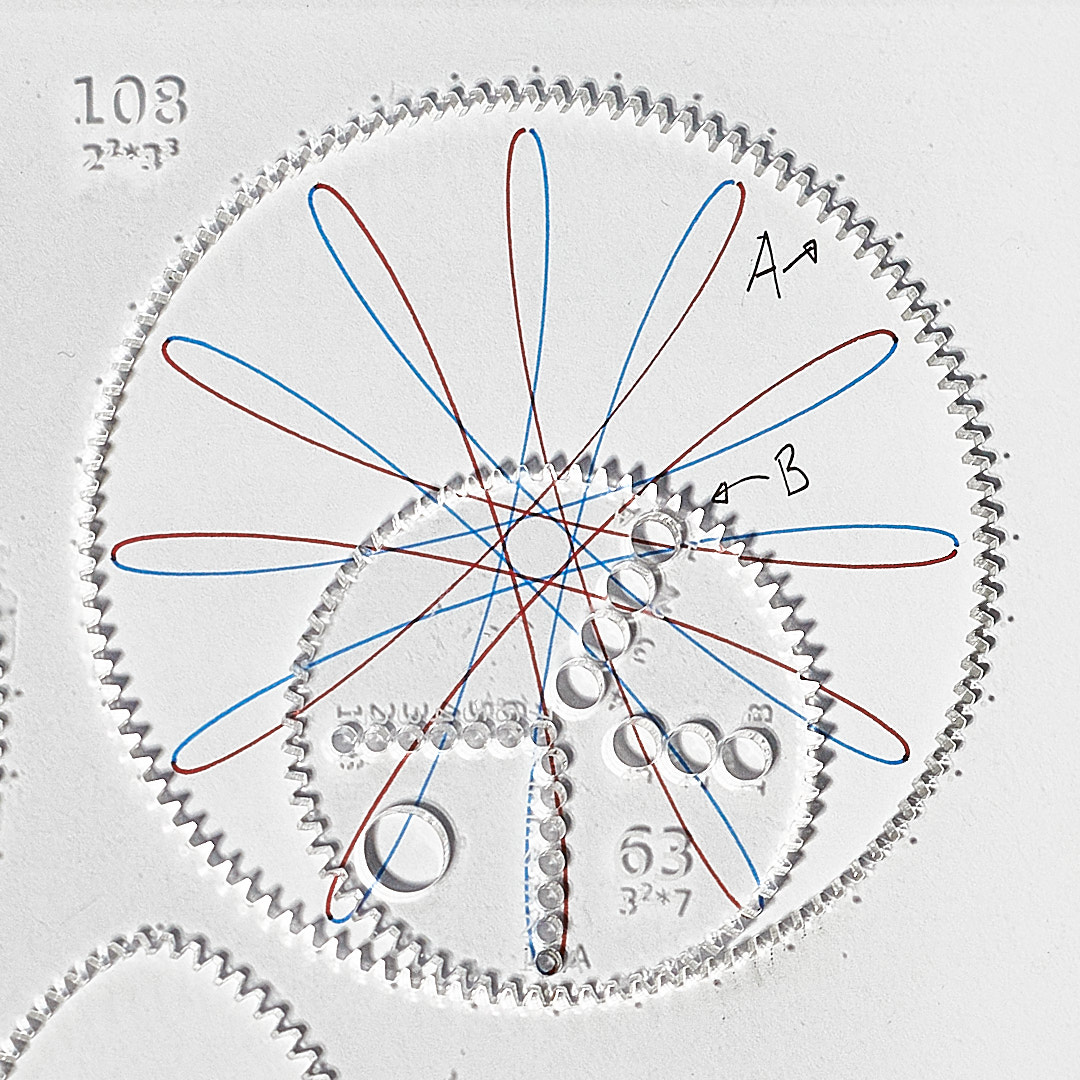 The line changes colour each time $\mathbf{B}$ rotates once (12 times)...
The line changes colour each time $\mathbf{B}$ rotates once (12 times)...
-
 ...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (7 times).
...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (7 times).
#### 1.1 The number of points in a simple system
In spirograph terms, the number of rotations of $\mathbf{B}$ for it to first return to the starting point is $A\over\gcd(A,B)$. This corresponds to the number of points.
We will notate this as:
$$ r(A,B) = \frac{A}{\gcd(A,B)} $$
Note that the number of rotations around $\mathbf{A}$ that $\mathbf{B}$ completes in this time is $r(B,A)$.
#### 1.2 The spacing between points in a simple system
The gap between the points is $\frac{A}{\text{number of points}}$, i.e. just $\gcd(A,B)$.
## 2 Compound Systems
In a compound pattern, a wheel $\mathbf{D}$ rotates inside a hole $\mathbf{C}$ cut from a wheel $\mathbf{B}$, which in turn rotates against a static $\mathbf{A}$, with teeth $D$, $C$, $B$, $A$ respectively.
Now we know from (1.1) that $\mathbf{B}$ will complete $r(A,B)=\frac{A}{\gcd(A,B)}$ rotations inside $\mathbf{A}$ before returning to its starting point, in which time $\mathbf{C}$ must also rotate the same number of times (since it is a different edge of the same piece). Thus, $\mathbf{D}$ must traverse some multiple of $C.r(A,B)$ teeth to return to the starting point.
Therefore let $n, m \in \mathbb{N}$ such that $nD = mC.r(A,B)$.
Following the same logic as in Section 1, we can write down
$$m = \frac{\lcm(D,C.r(A,B))}{C.r(A,B)}$$
$$n = \frac{\lcm(D,C.r(A,B))}{D}$$
Some rearrangement yields:
$$\lcm(D,C.r(A,B)) = \frac{\lcm(AC,BC,BD)}{B}$$
A curve produced by a simple system.
-
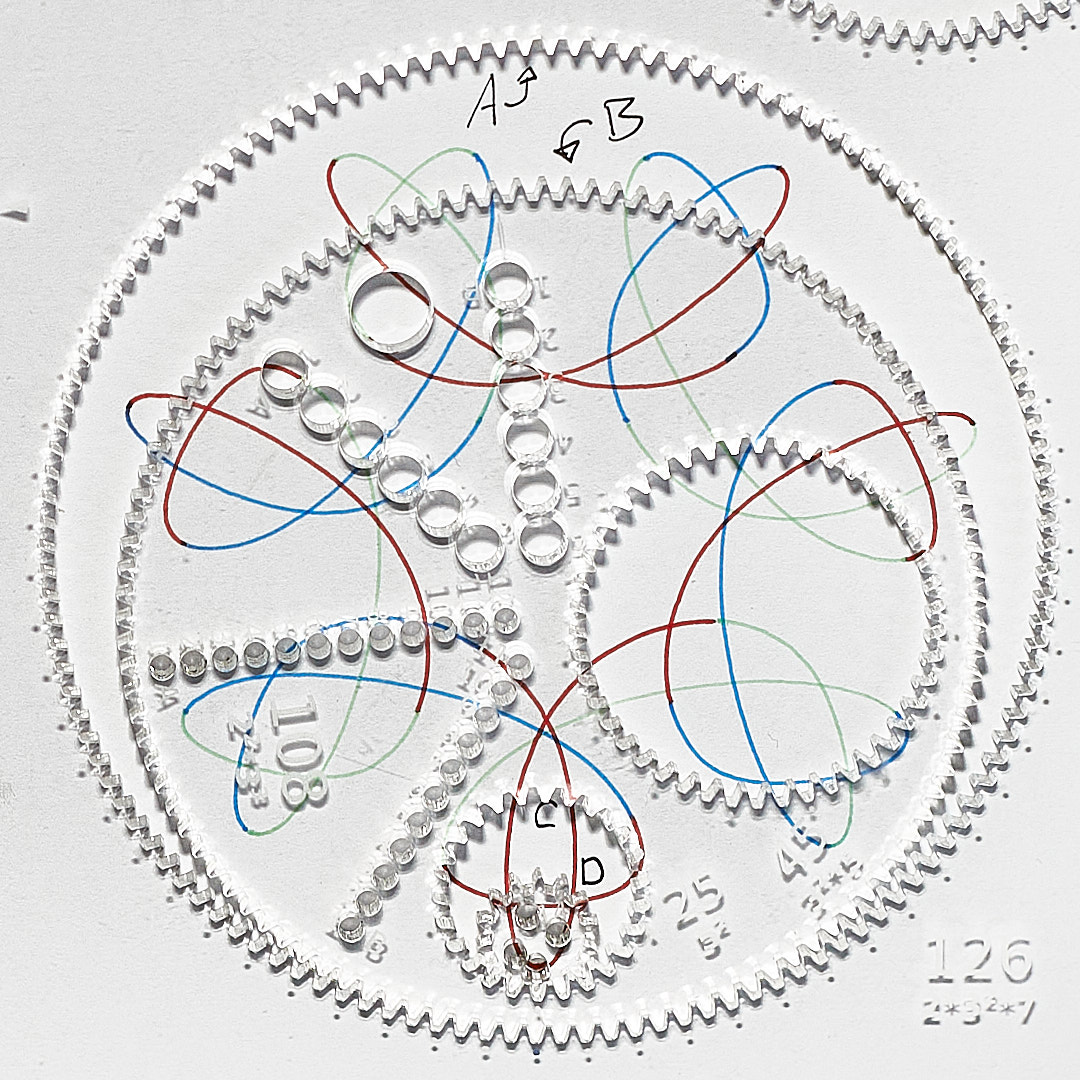 The line changes colour each time $\mathbf{D}$ rotates once (28 times)...
The line changes colour each time $\mathbf{D}$ rotates once (28 times)...
-
 ...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (14 times).
...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (14 times).
#### 2.1 The number of rotations of the smallest part in a 3-part system
The number of rotations of $\mathbf{D}$ is:
$$\frac{\lcm(AC,BC,BD)}{BD}$$
This will be the number of 'points' that the design has - although given the complexity of the movements involved, this may not be very visually apparent.
#### 2.2 The number of rotations of the middle part in a 3-part system
The middle component (outer edge $B$, inner edge $C$) must rotate $m.r(A,B)$ times, which is to say that the number of rotations is:
$$\frac{C\lcm(AC,BC,BD)}{B}$$
## 3 Wrapping up
I found these results handy for working out which combinations of wheels and rings to use in my spirographing; the next things I'm planning to do are write about symmetries of spirographs and maybe at some point share a spreadsheet automating these calculations.
I'm reasonably certain that the results here could form the basis for exploration of arbitrarily nested spirograph systems. The line changes colour each time $\mathbf{B}$ rotates once (12 times)...
The line changes colour each time $\mathbf{B}$ rotates once (12 times)...
 ...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (7 times).
...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (7 times).
 The line changes colour each time $\mathbf{B}$ rotates once (12 times)...
The line changes colour each time $\mathbf{B}$ rotates once (12 times)...
 ...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (7 times).
...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (7 times).
 The line changes colour each time $\mathbf{D}$ rotates once (28 times)...
The line changes colour each time $\mathbf{D}$ rotates once (28 times)...
 ...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (14 times).
...and here it changes colour each times $\mathbf{B}$ completes one circuit of $\mathbf{A}$ (14 times).